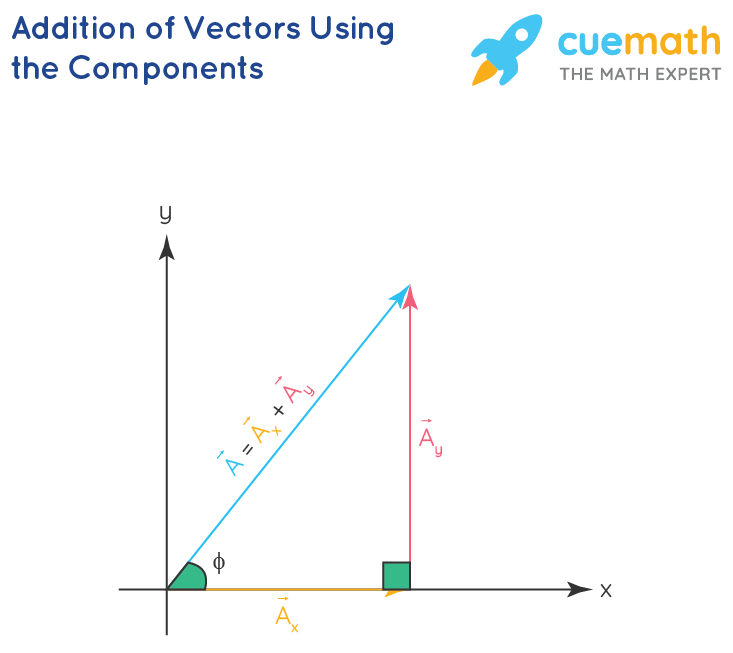
 Vector addition finds its application in physical quantities where vectors are used to represent velocity, displacement, and acceleration. Adding the vectors geometrically is putting their tails together and thereby constructing a parallelogram.
Vector addition finds its application in physical quantities where vectors are used to represent velocity, displacement, and acceleration. Adding the vectors geometrically is putting their tails together and thereby constructing a parallelogram. To add 2 vectors, add each of the components, or subtract them if you’re subtracting the vectors. For instance, to add 2-D vectors, you would just add both x components and both y components together.
To add 2 vectors, add each of the components, or subtract them if you’re subtracting the vectors. For instance, to add 2-D vectors, you would just add both x components and both y components together.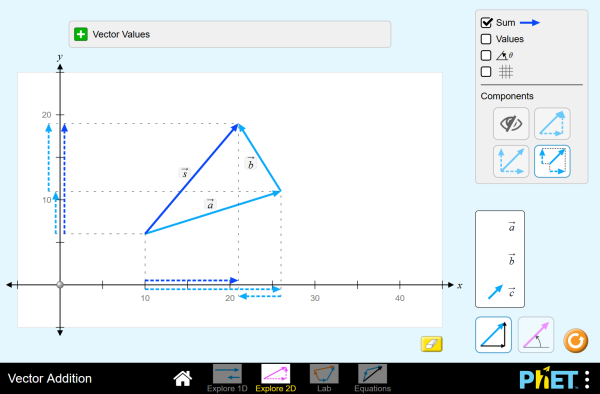 Explore vectors in 1D or 2D, and discover how vectors add together. Specify vectors in Cartesian or polar coordinates, and see the magnitude, angle, and components of each vector. Experiment with vector equations and compare vector sums and differences.
Explore vectors in 1D or 2D, and discover how vectors add together. Specify vectors in Cartesian or polar coordinates, and see the magnitude, angle, and components of each vector. Experiment with vector equations and compare vector sums and differences.